El mecanismo focal es una representación
gráfica de dos posibles soluciones de la ruptura
que origina un sismo (Figura 1) y de la
configuración de los esfuerzos
tectónicos en el área, es
decir, un compendio de informaciones que describen el
posible mecanismo de falla en la fuente o foco donde se
libera la energía en forma de ondas
sísmicas. |
|
| |
| |
|
Falla Transcurrente
|
Falla Normal
|
Falla Inversa
|
| |
|
|
|
| |
|
Figura 1. Mecanismos
focales de los principales tipos de fallas con sus
correspondientes configuraciones de esfuerzos.
|
[Ver más]
|
Método
para obtener
un Mecanismo Focal
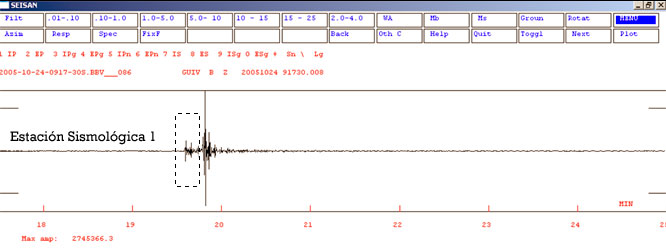
Uno de los métodos para obtener la
solución del mecanismo focal de un sismo consiste
en la identificación de la llamada "polaridad"
de las primeras llegadas que se registran en un
sismograma. Este procedimiento de lectura se
efectúa en cada una de las estaciones
sismológicas que registran el evento
sísmico. La polaridad , tal como se puede
apreciar en la figura 2, representa la
caracterización del primer pulso de la onda
registrada proveniente del sismo, en términos de
una compresión -pulso hacia arriba- o una
dilatación -pulso hacia abajo-.
|
| |
|
| |
|
| |
|
| |
|
| |
|
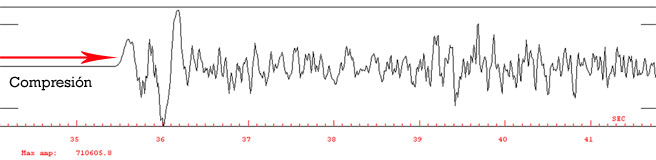
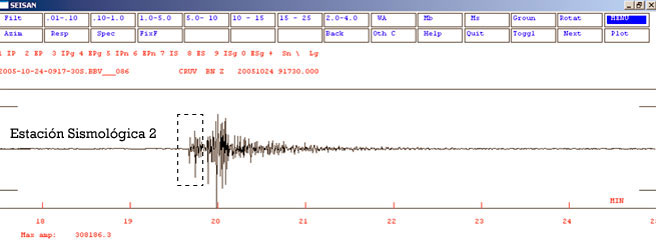
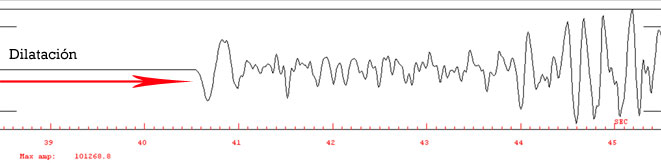
Figura 2.
Identificación de polaridad
-caracterización del primer pulso- en las primeras
llegadas provenientes de un sismo registrado en dos
estaciones sismológicas. En la parte superior se
observa una compresión -pulso hacia arriba-, y en
la imagen inferior una dilatación -pulso hacia
abajo-. Para ambos sismogramas se realiza un acercamiento
o zoom a las primeras llegadas o primer arribo de las
ondas para observar en detalle su polaridad asociada.
|
[Ver más]
|
Una vez concluida la revisión de los
sismogramas de todas las estaciones sismológicas,
se procede a graficar tal información en una red
estereográfica -plantilla de forma circular cuyo
centro representa el foco del evento sísmico-,
donde se asienta -con puntos- la ubicación de las
estaciones respecto al epicentro
y sus correspondientes polaridades (Figura 3).
|
| |
|
|
| |
|
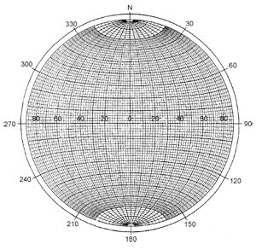
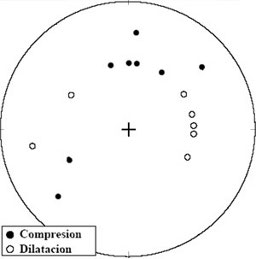
Figura 3. La
red estereográfica de Lambert-Schmidt -ubicada
a la izquierda- es donde se asientan los datos de po
laridad recopilados entre las diferentes estaciones
sismológicas que conforman la Red
Sismológica Nacional. Para lograr la
ubicación adecuada de los datos en la red
estereográfica es necesario contar con dos
parámetros: el azimut -ángulo medido desde
el norte, en el sentido de las agujas del reloj, de la
estación sismológica respecto al epicentro-
y el ángulo de salida de la onda que llega a la
estación medido desde su punto inicial (el foco) y
con respecto a la vertical. Toda esta información,
una vez graficada sobre la red, considerando la
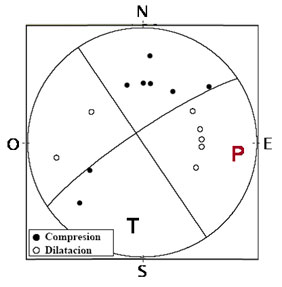
nomenclatura para la compresión -círculos
negros- y dilatación -círculos blancos-,
refleja una distribución como la que se muestra en
la figura de la derecha.
|
[Ver más]
|
|
Seguidamente, se realiza una separación de
las
áreas de acuerdo con los tipos de polaridades, es
decir, se separan las zonas de dilatación de las
de compresión o viceversa, generándose de
esta forma 4 cuadrantes delimitados por 2 planos que
deben ser perpendiculares entre sí (Figura 4).
|
| |
|

|
| |
|
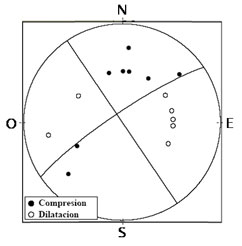
Figura 4. La separación
de las áreas de
compresión de las de dilatación -figura a
la izquierda- genera 4 cuadrantes delimitados por 2
planos también conocidos como planos nodales .
Su construcción final y representación
más general lleva al mecanismo focal ilustrado a
la derecha. |
| |
|
La separación de los cuadrantes o zonas de
compresión y dilatación resultan más
fiable a medida que se incrementa el número de
estaciones que aportan información de polaridades
y se logra una distribución adecuada de los puntos
a lo largo de toda la red estereográfica
-cobertura de 360º alrededor del epicentro-. Es por
ello que el mecanismo focal no puede obtenerse para todos
los eventos sísmicos que ocurren en el
país, y su realización depende de factores
tales como:
• La cobertura de estaciones
sismológicas existentes alrededor del epicentro.
• La magnitud
del evento sísmico.
• La posibilidad de efectuar lecturas
de
compresión y dilatación adecuadamente.
|
| |
| |
|
Proyección de los planos de las
fallas
en la esfera focal
|
|
El mecanismo focal corresponde con una vista en planta
del plano ecuatorial de una esfera cuyo centro representa
el foco del sismo, y en donde todas las proyecciones que
se registran en este plano corresponden con las
intersecciones que se efectúan en el hemisferio
inferior de la esfera (Figura 5).
|
| |
|
| |
|
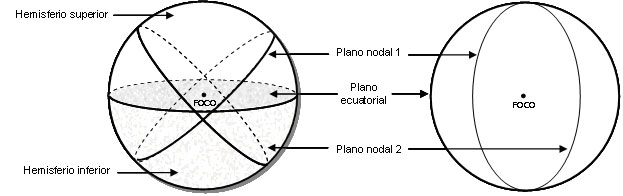
Figura 5.
Esfera focal con centro en el foco donde se ilustran los
hemisferios superior e inferior y el plano ecuatorial que
corta a la esfera en dos mitades iguales (izquierda de la
figura). A la derecha se observa la vista en planta del
plano ecuatorial con las correspondientes proyecciones de
la intersección de los planos nodales 1 y 2 con el
hemisferio inferior
|
[Ver más]
|
| Información que
se
obtiene de un Mecanismo Focal |
|
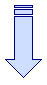
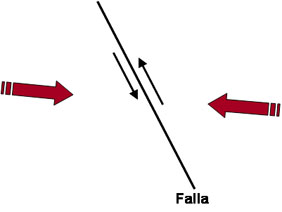
• Posible tipo de falla que originó el
sismo (Figura 6).
|
| |

|

|

|

|
|

|

|

|

|
|
|

|
|
Falla Transcurrente
|
Falla Normal
|
Falla Inversa
|
Falla Oblicua
Combinación de 2 tipos de fallas
(para el caso ilustrado: transcurrente con normal)
|
| |
|
Figura 6.
Representación de los mecanismos focales
más comunes y sus correspondientes fallas
generadoras
|
[Ver más]
|
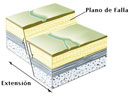
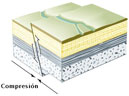
- Características geométricas de
la
falla (ver figura 7).
|
| |

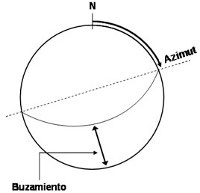
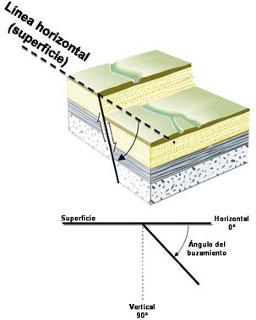
El buzamiento tiene relación directa con la
curvatura o "barriga" del plano. Su
cálculo se
lleva a cabo midiendo los grados que existen desde el
centro del plano hasta la superficie de la esfera. Para
el caso de un plano sin curvatura, es decir, una
línea recta, el valor del buzamiento
correspondería a 90º por ser ese el resultado
desde el centro de la esfera hasta cualquier punto en la
superficie de la misma.
|
 |
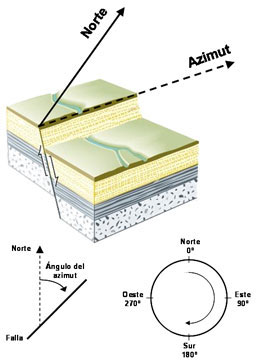
Uniendo los extremos del plano seleccionado con una
línea segmentada se determina la dirección
del azimut de la falla, y su valor en grados se obtiene
midiendo desde el norte, en el sentido de las agujas del
reloj, hasta la intersección con la línea
segmentada.
|
| |
|
|
|
|
| |
|
Figura 7.
Los diversos parámetros que describen la
geometría de la falla que originó el sismo
pueden extraerse del mecanismo focal obtenido para el
evento sísmico. Para ello debe definirse cual de
los 2 planos es el que corresponde con la falla donde se
produce la fractura (plano principal), y sobre
éste calcular el azimut siguiendo los pasos
descritos en la parte superior e inferior izquierda, y el
buzamiento como se ilustra en la parte superior e
inferior derecha
|
[Ver
más]
|
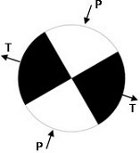
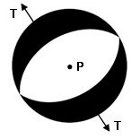
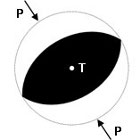
- Los ejes T , P y B que describen
los esfuerzos
tectónicos del
área (Figura 8).
|
| |
|
|
| |
|
Figura 8 .
Ubicación de los ejes T y P en la esfera focal;
los mismos se localizan a 45° de los polos de los
planos, asignando al eje T en el cuadrante de las
compresiones y el P en el de las dilataciones. El eje B
representa el eje nulo. Estos ejes representan los
esfuerzos tectónicos dominantes en el área
donde se produjo la ruptura. .
|
| |
|
|
| |
|
|
| |
|
|
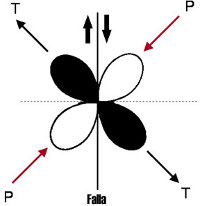
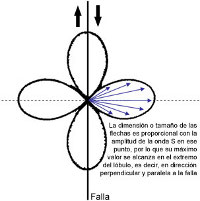
Figura 9.
Patrón de
radiación de la onda P y S
-izquierda y derecha respectivamente- basado en la
configuración de una falla transcurrente de
orientación dextral. El patrón de
radiación corresponde con una descripción
geométrica de la amplitud de la onda y su
distribución a lo largo del foco del sismo.
|
[Ver
más]
|
|
REFERENCIAS
- Ammon, C., (2001). Faults and Faulting
http://eqseis.geosc.psu.edu/~cammon/HTML/Classes/IntroQuakes/Notes/faults.html
[En línea]. (Consultado agosto 7, 2006).
- Bormann, P., (2002). New Manual of Seismological
Observatory Practice (NMSOP). GeoForschungsZentrum
(GFZ), Potsdam - Alemania. Vol. 1, capítulo 3:
58-68.
- Cronin, V., (2004). A Draft Primer on Focal
Mechanism Solutions for Geologists. Universidad de
Baylor, Texas - EE.UU.
http://serc.carleton.edu/files/NAGTWorkshops/structure04/Focal_mechanism_primer.pdf
[En línea]. (Consultado agosto 7, 2006).
- Ichinose, G., Frohlich, C. y Oppenheimer, D., (En
construcción). Focal Mecanism
http://www.seismo.unr.edu/htdocs/WGB/Recent/explanation/
[En línea]. (Consultado agosto 7, 2006).
- Lay, T. y Wallace, T., (1995). Modern Global
Seismology. Academic Press, San Diego - EE.UU.
capítulo 8: 346-354.
- Nava, A., (1998). La Ciencia para Todos
http://bibliotecadigital.ilce.edu.mx/sites/ciencia/volumen3/ciencia3/113/htm/sec_7.htm
[En línea]. (Consultado agosto 7, 2006).
|
