|
EL TERREMOTO DE CARACAS Y EL MODELAJE DE ESCENARIOS SISMICOS APLICACION A UN SISTEMA DE PRODUCCION DE AGUA POTABLE. José Grases G.
RESUMEN Una de las características que distingue los terremotos de otras amenazas naturales, aparte de la incapacidad en la cual nos encontramos para su predicción, es la extensión de la zona en la cual los efectos suceden de modo simultáneo. Para magnitudes de cierta importancia, las áreas en las cuales la intensidad de los movimientos alcanzan valores elevados pueden ser de varios miles de kilómetros cuadrados. En este trabajo se tratan los problemas asociados al cálculo de la confiabilidad de un sistema de producción de agua potable, con una capacidad de 7 metros cúbicos por segundo, que debe elevar esa cantidad de agua desde el nivel de producción (160 m sobre el nivel del mar) hasta el nivel de consumo (1000 m sobre el nivel del mar); esto, a lo largo de una tubería de unos 56 km, con diámetros de hasta 72", pasando por una topografía con fuertes irregularidades en su trazado, parcialmente salvada con túneles y puentes. Por razones hidráulicas, en adición a las bombas y tanques de succión, el sistema requiere chimeneas de equilibrio con alturas de hasta 98 metros; la energía que permite su funcionamiento se asegura por medio de una red con un nivel de tensión de 215 KV, reducido a 6,6 KV en subestaciones con equipos tradicionales. En el modelaje de escenarios sísmicos se consideró la historia de sismos sucedidos en los últimos 120 años, para los cuales se ha recabado información sobre la extensión y atenuación de sus efectos; entre estos últimos, el que ofrece mejor información es el terremoto del 29 de Julio de 1967. El modelaje de la vulnerabilidad combinó información estadística, con el resultado de estudios analíticos de algunos de los 10 componentes mas importantes del sistema. Los resultados del estudio de confiabilidad, permiten identificar los elementos que mas contribuyen a la eventual disrupción del sistema por la acción de sismos. 1.- INTRODUCCION Las estadísticas sobre daños
debidos a sismos en los sistemas de transporte, almacenamiento, tratamiento
y distribución de agua, son una valiosa fuente de información,
pues orienta sobre aspectos críticos a ser analizados con más
detenimiento en este tipo de sistema. En la Tabla 1.1 se presenta un resumen
de casos identificados entre 1985 y 1995; una versión más
detallada se da en la Referencia 24.
TABLA 1.1 SISMOS QUE HAN AFECTADO SISTEMAS DE AGUA POTABLE Y TRANSPORTE DE LIQUIDOS (1985-1995) (FUENTE: REF. 24)
Típicamente, un sistema de producción de agua potable puede ser descrito por los elementos indicados en la Figura 1.1 En este trabajo se evalúa la confiabilidad de un determinado sistema, entendida como complemento de la probabilidad de falla o de interrupción de suministro. 2.- CONFIABILIDAD DEL SISTEMA 2.1.- CONCEPTOS BASICOS Con la información disponible para caracterizar el sistema, se pueden emplear métodos simplificados para el cálculo de la confiabilidad (Ref. 5). Esta es el complemento de la probabilidad de falla, entendiendo por esta un estado en el cual el sistema deja de cumplir sus funciones. Si se designa por (Ei) el evento falla según el modo i, la probabilidad de falla es igual a: Pfalla = P [E1 U E2 U E3 ......... U En] (2.1) donde la unión U debe realizarse para todos los modos relevantes. Si se designa por (Pfi) la probabilidad de falla asociada al evento (Ei), las dos cotas siguientes se satisfacen: Pfalla ³
máx (P¦
i)
(2.2)
FIGURA 1.1 ESQUEMA TIPICO DE UN SISTEMA DE PRODUCCION
No se puede descartar que en el sistema la intersección de modos de falla, la cual se designa por (n ), sea nula; es decir, en general. P [Ei n Ej ] > 0 (2.4) Los dos límites dados por las ecuaciones (2.2) y (2.3) se encuentran relativamente alejados. Si todas las probabilidades relevantes de falla son suficientemente pequeñas, o sea: para toda i la (P¦ i) << 1,0, una buena aproximación de la ecuación (2.3) resulta ser: Pfalla @ 2.2.- CONFIGURACION - Sistemas en Serie
La confiabilidad del sistema total (1-ps) es igual a: (1-ps) = donde (P¦ i) es la probabilidad de que el componente no se comporte satisfactoriamente; o sea, falle. Sí:
se puede aceptar que la confiabilidad del sistema es: (1-ps) @ 1 - que es similar a (2.3a). - Sistemas Redundantes en Paralelo
El sistema se comporta satisfactoriamente siempre que uno cualquiera de los componentes no falle. Para eventos (Ci) independientes, la confiabilidad del sistema es: (1-ps) = 1 - ( - Sistemas Mixtos El caso más sencillo puede ilustrarse
con tres componentes según el arreglo que sigue.
Para eventos independientes, la confiabilidad del sistema (1-ps) es: (1-ps) = (1-P¦ i) (1-P¦ 2 . P¦ 3) (2.8) En el caso ilustrado, la adición del componente 3, redundante, con (P¦ 3 < 1,0), da lugar a un sistema más confiable que aquel en el cual no estuviera presente, cuya confiabilidad es: (1-ps) = (1-P¦ 1).(1-P¦ 2) (2.9) 2.3.- INCORPORACION DE LA VULNERABILIDAD Haciendo uso del Teorema de probabilidad total (Ref. 5): P [Df]
= P [Df n
I1]
+ P [Df n I2]
+...... + P [Df
n In]
= donde: (Df) representa el estado de falla. Recordando que: P [Df n I j ] = P [Df / I j] x P [I j ] (2.11) se obtiene: P [Df ] = ecuación que será empleada para el cálculo de las probabilidades de falla. 3.- DESCRIPCION DEL SISTEMA, AMENAZAS NATURALES Y CARACTE-RIZACION DE LA VULNERABILIDAD A LAS ACCIONES SISMICAS 3.1.- DESCRIPCION DEL SISTEMA La ubicación geográfica del Sistema estudiado se da en el Mapa 3.1 y en la Figura 3.1 se presenta un diagrama esquemático con los cambios de elevación. El sistema consta de: 2 represas, 5 estaciones de bombeo, 4 puentes sobre 3 ríos diferentes, 8 chimeneas de equilibrio verticales (alturas entre 20 y 98 m), 3 túneles, 2 plantas de pretratamiento cercanas a las tomas del río Tuy y 1 planta de tratamiento justo antes del Sistema de Distribución (Refs. 23; 17). 3.2.- AMENAZAS NATURALES 3.2.1.- VIENTOS Es bien sabido que la distribución de velocidades máximas de viento, depende de la duración del registro. A fin de poder comparar los datos suministrados a partir de estaciones venezolanas (Ref. 10), con datos de las Antillas Menores (Ref. 11), se adoptó como velocidad el valor promedio durante 10 minutos de registro continuo. Para el área de interés la distribución de valores extremos de la velocidad del viento (V) es igual a: F (V, t) = P (V £ v,t) = Donde: t = Vida útil considerada (años); 0,282 y 10 (m/seg) = Valores característicos del área de los Valles del Tuy. Los registros arrojan medias mensuales entre 5- 0 mm, hasta algo más de 100 mm en períodos lluviosos. La precipitación acumulada anual va desde unos 800 mm/año a unos 1000 m.s.n.m. hasta cerca del doble en las cotas más bajas del área (Ref. 3). 3.2..3- CAUDALES EXTREMOS Dos de los puentes del sistema estudiado se encuentran sobre el Río Guaire; la distribución promedio de valores extremos anuales del caudal (Q) entre 5 y 500 años (Ref. 27) puede ser descrita de acuerdo a la expresión: F (Q £ q) = donde q es un valor particular del caudal Q, entendido como variable aleatoria. 3.2.4.- SISMOS - Movimientos Máximos del Terreno En las áreas al norte del Sistema, las aceleraciones máximas del terreno (Ao) están asociadas a la siguiente función de distribución acumulada (Ref. 16): FA (Ao) = P En las áreas más al sur esta función vale: FA (Ao) = P Los efectos de topografía se han evaluado de acuerdo a la Ref 1. - Intensidades de Mercalli Por múltiples razones, el empleo de los grados de la escala de Mercalli (IMM) no puede obviarse. Para ello se emplearon las correlaciones con Ao propuestas en la Ref. 1 que son las siguientes: log10 (Ao) = 0,30 (IMM) media (3.5a) log10 (Ao) = 0,30 (IMM + 1) media + 1s (3.5b) log10 (Ao) = 0,30 (MMI + 2) media + 2s (3.5c) donde s es la desviación estándard. - Formas Espectrales En los análisis dinámicos hechos se emplearon las formas espectrales normalizadas de la Ref. 9. - Deslizamientos Con los datos recopilados (en la Ref. 20), el área (A) en km2 que como máximo es afectada por deslizamientos de tierra, está aproximadamente relacionada a la magnitud (Ms) por la relación: log A = 1,78 + 1,29 (Ms - 5)0,829 5 £ Ms £ 8 (3.6) Aún cuando estas áreas generalmente no son circulares, a los fines de las evaluaciones de escenarios se supondrán circulares. De ese modo, la regresión anterior se puede expresar en función de la distancia epicentral (D) en (km) como: log D = 0,94 + 0,64 (Ms - 5)0,829 (3.7) 3.4.- CARACTERIZACION DE LA VULNERABILIDAD A LAS ACCIONES SISMICAS 3.4.1.- REPRESAS Las represas de concreto han mostrado una
gran reserva resistente. La estadística conocida sobre el desempeño
de represas de tierra reporta más casos de daños por sismos;
en parte, esto se debe a que son más numerosas que las de concreto.
El vector para el estado de daño (Df) para las represas
del sistema, está basado en la estadística de 456 represas
de tierra (Ref. 8) y se da en la Tabla 3.1.
TABLA 3.1 VECTORES DE PROBABILIDAD CORRESPONDIENTE A ESTADOS DE DAÑO SEVEROS Y/O RUINA (SISMO EN EPOCA DE ESTIAJE)
(1) Chimeneas de equilibrio; (2) Represa de tierra; (3) Tuberías en plano; (4) Tuberías en ladera; (5) Estación de bombeo; (6) Puentes; (7) Túneles; (8) Planta de tratamiento 3.4.2.- TUBERIAS Para las tuberías de mayor diámetro con estadísticas publicadas, sobre los efectos de sismos, se han adoptado los valores dados en las Refs. 2; 6 y 26 (Tabla 3.1). 3.4.3.- PUENTES La vulnerabilidad de estos componentes se considera limitada. Esta se ha modelado con los valores dados en la Ref 4 (Tabla 3.1). 3.4.4.- CHIMENEAS DE EQUILIBRIO En base a evaluaciones analíticas, la vulnerabilidad de estos elementos se caracterizó en términos de la demanda de ductilidad D: demandas D en exceso de 2,25, se asociaron a una elevada probabilidad de ruina. Las aceleraciones del terreno se expresaron en términos de (IMM) con arreglo a la Sección 3.2.4. Las acciones eólicas representan un riesgo inferior a las sísmicas. 3.4.5.- RED DE ALTA TENSION Para los equipos de 215 KV utilizados, los elementos de porcelana de las S/E poseen una alta vulnerabilidad. De acuerdo a la Ref. 14, para equipos frágiles la probabilidad esperada de falla en base a una estadística de 1400 equipos dañados, resultó ser: Pf = 0,21 + 0,43 (Ao/g) 0,05g £ Ao £ 0,90g (3.8) 3.4.6.- ESTACIONES DE BOMBEO De acuerdo a la Ref 22 la tasa de fallas de bombas centrífugas es de 1,71 x 10-2 (1/año). Si P es la probabilidad de falla de un componente y hay n componentes idénticos, la probabilidad de que falle alguno es 1-(1-P)n. Los tanques de succión representan elementos menos riesgosos que los equipos de las S/E, los cuales esencialmente condicionan la vulnerabilidad. 3.4.7.- TUNELES Las probabilidades de falla en túneles de tubería forzada se consideran muy pequeñas (Ref. 21 y 13). 3.4.8.- VECTORES DE PROBABILIDADES DE FALLA La Tabla 3.1 sintetiza la información acopiada sobre los componentes del sistema. 4.- SELECCION DE ESCENARIOS Y CONFIABILIDAD DEL SISTEMA 4.1.- Selección de Escenarios Sísmicos De acuerdo a los patrones medios de atenuación de Intensidades de Mercalli de sismos de la región a lo largo del último siglo, el área puede ser afectada por dos tipos de familias de sismos con Intensidades de Mercalli hasta del Grado VIII a IX; estas familias pueden ejemplificarse así: (a) eventos con epicentros locales tipo (1878, con Ms asignada de 6; 1969, con mb = 4,6) y (b) eventos con epicentro mayoritariamente submarino, a distancias intermedias tipo (1900, con Ms = 7,6; 1915, con mb =5,6; 1921, con mb = 4,8; 1960, con mb = 4,9; 1967, con Ms = 6,6) (Ref. 15). 4.2.- CALCULO DE LA CONFIABILIDAD Tomando en consideración la configuración de los componentes del Sistema, se emplearon las expresiones para sistemas en serie con un total de 32 componentes. A continuación se dan los resultados de dos ejemplos: Ejemplo 1: Sismo local sobre la falla de Tácata, con intensidad de Mercalli Grado VIII hasta la CH 22 (véase la Figura 3.1), Mercalli Grado VII hasta el Túnel del Km 20-21, y Mercalli Grado VI hasta la Planta de Tratamiento de La Guairita. Para este evento, comparable a otros reportados en la región, la confiabilidad del sistema resulta ser igual a 0,46; es decir la probabilidad de que el sistema deje de operar es bastante elevada (0,54). Los componentes que más contribuyen en este resultado son los que se encuentran ubicados en el área de mayor Grado de Intensidad (Grado VIII); entre ellos: la represa de tierra y las tuberías en ladera. Ejemplo 2: Repetición del sismo de 1900, con intensidad de Mercalli Grado VII en todo el sistema (Ref. 19). La confiabilidad resulta ser igual a: 0,745. La probabilidad de falla obtenida (0,255) es mitad que la obtenida en el Ejemplo 1. Como comentario, procede señalar
que la mayor utilidad de la metodología descrita, se encuentra en
la posibilidad de evaluar cuantitativamente la influencia de modificaciones,
mejoras o trazados alternos en la respuesta esperada del sistema. Su extensión
a los tiempos probables de rehabilitación del sistema es inmediata,
sea para sismos o para otras causas de disrupción, siempre que se
disponga de estadísticas confiables sobre los diferentes tipos de
averías.
REFERENCIAS 2. ARIMAN T., LEE B. and CHEN Q. (1987) Failure of Buried Pipelines under Large Ground Deformations. In: ARIMAN et al., Recent Advances in Lifeline Earthquake Engineering, Developments in Geotechnical Engineering, vol 49. Elsevier, Amsterdam. 3. ARMADA DE VENEZUELA (1997) Precipitación mensual en la Estación Meteorológica Observatorio Cagigal (1947-1996). Dirección de Hidrografía y Navegación, Caracas. 4. ATC-13 (1985) Earthquake Damage Evaluation data for California. Redwood City, 483p 5. BENJAMIN J. R. and CORNELL A.C. (1970) Probability, Statistics and Decision for Civil Engineers. McGraw Hill, New York, 684p 6. BUILDING SEISMIC SAFETY COUNCIL (BSSC) (1987) Abatment of Seismic Hazards of Lifelines: Proceedings of a Workshop on Developments of an Action Plan. Vol 5, Papers on Gas and Liquid Fuel Lifelines and Special Workshop Presentations. FEMA-139, July, Washington D.C. 7. CENTRE OF ADVANCED ENGINEERING (CAE) (1991) Lifelines in Earthquakes. Wellington Case Study. University of Canterbury, New Zealand, 39p. 8. CHANG, B.Q., CHEN R.F. and WU P. (1992) Preliminary evaluation of seismic risk of earth dams. Proc Tenth World Conf on Earthq Eng, Madrid, vol 1, 467-470. 9. COVENIN 1756 (1982) Edificaciones Antisísmicas. FONDONRMA, Caracas, 67p + comentarios. 10. COVENIN 2003 (1986) Acciones del Viento sobre las Construcciones. FONDONORMA, Caracas 48p + comentarios. 11. CUBIC (1989) Structural design requirements. Wind Load. Caribbean Uniform Building Code, Part 2, Section 2. Georgetown, 54p 12. DAVIS, F.F. et al (1982) Earthquake planning scenario for a magnitude 8.3 earthquake on the San Andreas fault in the San Francisco bay area. California Department of Conservation, Division of Mines and Geology. Special Publication 61, 160p. 13. EARTHQUAKE ENGINEERING RESEARCH INSTITUTE (EERI) (1986) Reducing Earthquake Hazards: Lessons Learned from Earthquakes. Publication No 86-02, El Carrito, 208p. 14. EIDINGER, J., OSTROM, D. and MATSUDA, E. (1995) High Voltage Electric Substation Performance in Earthquakes. Proc 4th US Conf Lifelines Earthq Eng, San Francisco, 336-346. 15. GRASES J. (1980) Investigación sobre los Sismos Destructores que han afectado el Centro y el Occidente de Venezuela. Proyecto INTEVEP, 3 tomos, Caracas. 16. GRASES J., MALAVER A., LOPEZ S. and RIVERO P. (1995) Seismic Hazard Evaluation for Design and/or Verification of a High Voltage System. Proc 4th U.S. Conf on Lifeline Earthq Eng, San Francisco, August 10-12 17. GRINSTEINS, V. (1997),. Elevación (m.s.n.m.) versus Progresivas (km) Tuy I, Tuy II y Tuy III (VGE 22-12-96). Caracas, 40 p. 18. HOPKINS, D.C., LUMSDEN, J.L. and NORTON, J.A. (1993) Lifelines in Earthquakes. A Case Study based on Wellington. Bull of the New Zealand National Society for Earthquake Engineering, vol 26, No2, June, 208-221. 19. JAKUBOWICZ F., E y LAROTTA S., J. (1974). Terremoto del 29 de Octubre de 1900. Presentado en el I Congreso Venezolano de Sismología e Ingeniería Sísmica. Caracas. En: Boletín Técnico IMME 11 (47): 23-78. 20. KEEFER D.K. (1984) Landslides caused by earthquakes. Bull Geol Soc of America, 95, 406-421. 21. OWEN, G.N. and SHOLL, R.E. (1981) Earthquake Engineering of Large Underground Structures. JAB-7821. San Francisco: URS/John A. Blume . Citado por: St JOHN C.M. and ZAHRAH T.F. (1987) Aseismic Design of Underground Structures. Tunelling and Underground Space Technology, 2:2, 165-197. 22. PDVSA (1993) Manual de Ingeniería de Riesgos, Volumen 1. Criterios para el Análisis Cuantitativo de Riesgos. IR-S-02. Caracas, Mayo, 92p. 23. PIERETTI, J.G. (1965) Proyecto del Sistema de Bombeo Tuy No 2. Memoria Descriptiva, vol I, 97p; vol II y vol III planos, ediciones Plinio Alfonzo, Caracas. 24. RAMIREZ B. (1997) Plan de Emergencia para Atender Situaciones de Desastre en el Acueducto Metropolitano de Caracas, ante Averías ocurridas en el Sistema de Producción. Trabajo Especial de Grado para optar al Titulo de MSc en Ingeniería Sanitaria, UCV (en preparación). 25. SEED, H. and IDRISS, I. N. (1982). "Ground Motions and Soil Liquefaction During Earthquakes." Monograph Published by Earthquake Engineering Research Center, University of California at Berkeley, 134 p. 26. SHINOZUKA M., MURATA M. and IWATA T. (1992) Strategies for repair and restoration of seismically damaged gas pipeline systems. Proc 4th US-Japan Workshop on Earthquake Disaster Prevention for Lifeline Systems, NIST Spec Public 840, Washington, 391-405. 27. SUAREZ M. (1997) Comunicación personal. 28. WELLS, D. and COPPERSMITH, K. (1994) New empirical Relationships among Magnitude, Rupture Length, Rupture Width, Rupture Area and Surface Displacement. Bull Seism Soc of America, 84:4, 974-1002. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||

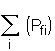 (2.3a)
(2.3a)



